1909年(明治42年)東京帝國大學工科大學-數學[5] - [別館]球面倶楽部零八式markIISR

[5] The gas envelope of a divigible balloon has the form of a surface of revolution. The parts $\mbox{AB},\mbox{CD}$ of the generating line $\mbox{ABCD}$ are parabolas with their axis to the axis $\mbox{AD}$ and their vertices at $\mbox{B},\mbox{C}$ respectively. The part $\mbox{BC}$ is a straight line parallel to the axis $\mbox{AD}$ . Find the distance of the center of the enclosed volume from the middle point of the whole length and its lifting power in pounds when it is filled with hydrogen gas, the air weighing $0.0763$ pounds and the hydrogen $0.0053$ pounds per cubic ft.

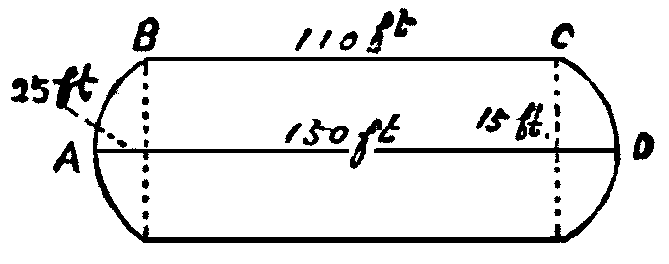
( $\mbox{BC}=110$ ft. , $\mbox{AD}=150$ ft. , $\mbox{BC}=15$ ft. , $\mbox{B}$ から $\mbox{A}$ への奥行が $25$ ft., $\mbox{C}$ から $\mbox{D}$ への奥行が $15$ ft.,)

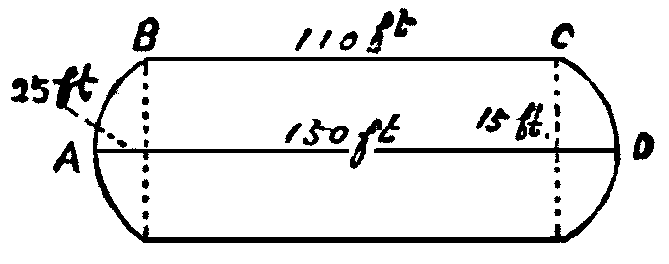
2019.04.08記

lifting power は、浮び上がろうとする力と訳した。浮力の英語は一般に buoyancy であり、 lifting power は揚力と訳すことが多いが、一般的に使われる揚力は移動している物体が浮かび上がろうとする力を指すので、与えられた条件から、文脈的に違うと判断した。放物線の軸が $\mbox{AD}$ なのに頂点が $\mbox{B},\mbox{C}$ というのは問題文がおかしいので、頂点が $\mbox{A},\mbox{D}$ とした問題を考える。

[5]分割できる気球からなるガス容器は回転面の形状をしている。母線 $\mbox{ABCD}$ の $\mbox{AB},\mbox{CD}$ の部分は軸が $\mbox{AD}$ の放物線であり、その頂点はそれぞれ $\mbox{A},\mbox{D}$ である。 $\mbox{BC}$ は、軸 $\mbox{AD}$ に平行な直線である。体積の中心から全長の中心までの距離および、容器が水素ガスで満たされているときの浮びあがる力を求めよ。ここで、1立方フィート当たり空気は $0.0763$ ポンド、水素は $0.0053$ ポンドとする。

$\mbox{A}(0,0)，\mbox{B}(25,r)，\mbox{C}(135,r)，\mbox{D}(150,0)$ とする。
回転放物面からなる立体の体積の切り口の半径がルートに比例するので、断面積は半径に比例することに注意すると、回転放物面からなる立体の体積は円筒の半分、重心の位置は頂点からの奥行の $\dfrac{2}{3}$ となる(三角形を想像せよ)。

よって容器の容積は、 $130 \pi r^2$ であり、重心の $x$ 座標は、 $\dfrac{\dfrac{25}{2}\cdot\dfrac{50}{3}+110\cdot 80+\dfrac{15}{2}\cdot 140}{130}=\dfrac{6035}{78}$ となる。
よってこれと全長の中心 $(75,0)$ との距離は $\dfrac{185}{78}$ となる。

単位体積あたりの浮力は $0.0710ポンド/立方フィート$ だから、これに体積を掛ければ良いが、体積を求める情報がないので求まらない。

2022.06.02記

[解答]
$\mbox{A}(0,0)，\mbox{B}(25,r)，\mbox{C}(135,r)，\mbox{D}(150,0)$ とすると，
$\rm AB$ は $y=\dfrac{r}{25}\sqrt{25x}$ ，
$\rm BC$ は $y=r$ ，
$\rm CD$ は $y=\dfrac{r}{15}\sqrt{15(150-x)}$
で表されるので，断面積 $f(x)$ は
$\dfrac{f(x)}{\pi r^2}=\left\{\begin{array}{ll} \dfrac{x}{25} & (0\leqq x\leqq 25) \\ 1 & (25\leqq x\leqq 135) \\ \dfrac{150-x}{15} & (135\leqq x\leqq 150) \end{array}\right.$
となる．よって体積の重心を $(g,0)$ とおくと
$g \displaystyle \int_0^{150} f(x)dx =\int_0^{150} xf(x)dx$
が成立する．
$\displaystyle \int_0^{150} f(x)dx =\dfrac{25}{2}+110+\dfrac{15}{2}=130$
であり，
$\displaystyle \int_0^{150} xf(x)dx$
$=\Bigl[ \dfrac{x^3}{75} \Bigr]_{0}^{25}$ $+\Bigl[\dfrac{x^2}{2}\Bigr]_{25}^{135}$ $+\Bigl[-\dfrac{225x^2-x^3}{45} \Bigr]_{135}^{150}$
$=\dfrac{625}{3}+\dfrac{160\cdot 110}{2}+\dfrac{225\cdot 285\cdot 15 - 15^3(1000-729)}{45}$
$=\dfrac{625}{3}+8800+75\cdot 14$
であるから，
$g=\dfrac{\dfrac{625}{3}+8800+75\cdot 14}{130}=\dfrac{6035}{78}$
となる．よって全長との中心との距離は $\dfrac{185}{78}$

後半の浮力に関する部分は物理なので放置しておく．