1925年(大正14年)東京帝國大學工學部-數學[3] - [別館]球面倶楽部零八式markIISR

2022.08.11記

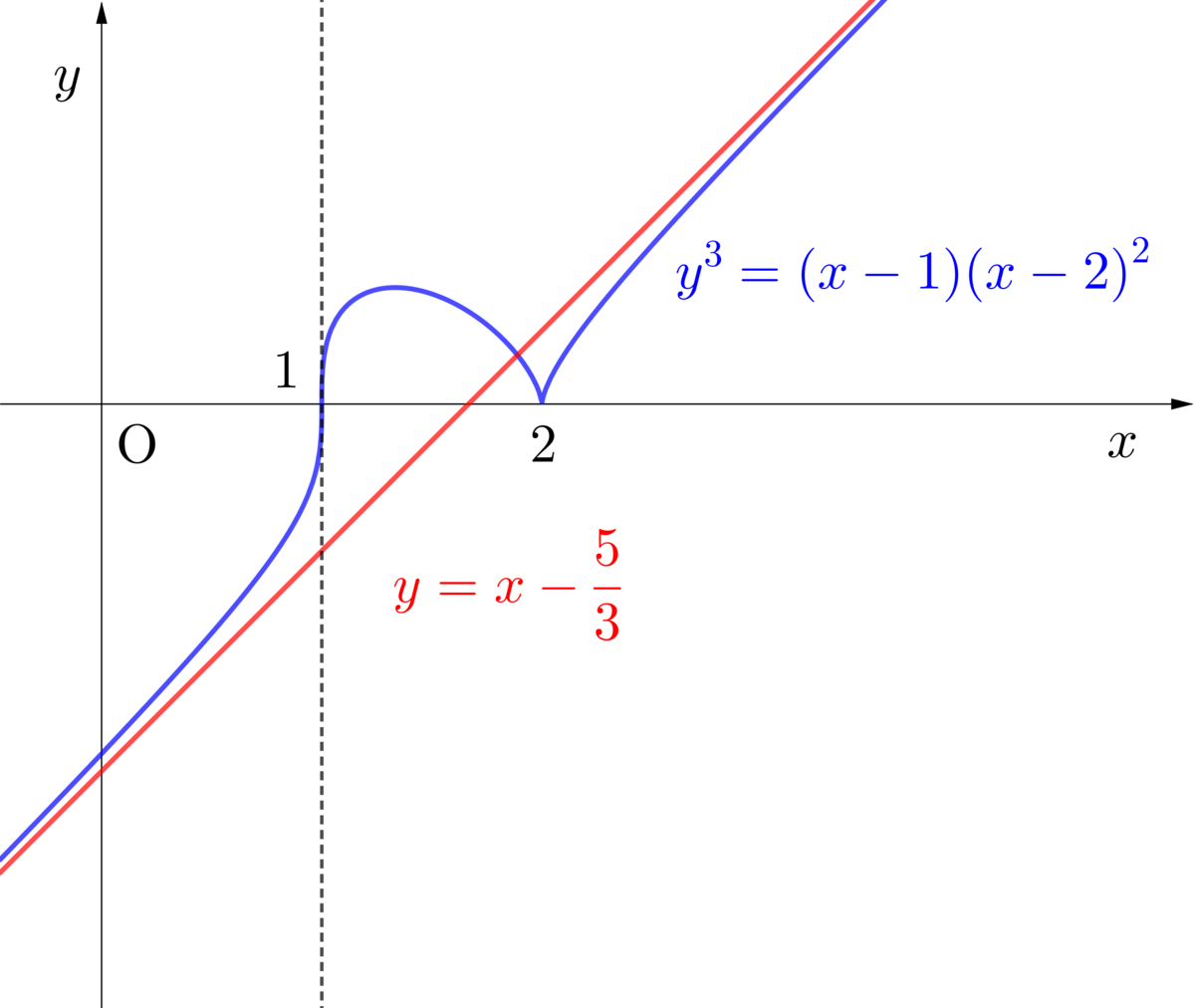
[3] 次ノ式ガ表ハス曲線ヲ畫ケ．
$y^3=(x-1)(x-2)^2$

2022.08.15記
$Y=(x-1)(x-2)^2$ のグラフを縦に3乗根をとることによっておおまかな形をとらえることができる(極値を与える $x$ の値は等しい)が，その際 $|x|$ が十分大きいときに
$y^3\approx x^3$ が成立することから， $y=x+K$ の形の漸近線をもつことに注意する．また， $x=2$ で二重解を三乗根をとることになるので， $x=2$ 近辺では $x-1\approx 1$ より $y\approx (x-2)^{2/3}$ だから， $(2,0)$ が尖点となることに注意する．

と，注意点が多いので普通に微分した方が細かいことを気にしなくて良い．

[解答]
$y=\{(x-1)(x-2)^2\}^{1/3}$
を微分すると
$y'=\dfrac{1}{3}\{(x-1)(x-2)^2\}^{-2/3}\cdot \{(x-1)(x-2)^2\}'$ $=\dfrac{3x-4}{3}\{(x-1)^2(x-2)\}^{-1/3}$ ，
$y''=\{(x-1)^2(x-2)\}^{-1/3}$ $-\dfrac{3x-4}{9}\{(x-1)^2(x-2)\}^{-4/3}\cdot (3x-5)(x-1)$
$=\dfrac{9(x-1)(x-2)-(3x-4)(3x-5)}{9}\{(x-1)^{-5}(x-2)^{-4}\}^{1/3}$
$=\dfrac{-2}{9}\{(x-1)^{-5}(x-2)^{-4}\}^{1/3}$
となるので
$\displaystyle\lim_{x\to\pm\infty} y'=1$ に注意すると
増減表は

$x$	$-\infty$	$\cdots$	$1$	$\cdots$	$\dfrac{4}{3}$	$\cdots$	$2$	$\cdots$	$+\infty$
$y'$	$1$	$+$	$+$	$+$	$0$	$-$	$-\infty$ ／ $+\infty$	$+$	$1$
$y$	$-\infty$	$\nearrow$	$0$	$\nearrow$	$\dfrac{\sqrt[3]{4}}{3}$	$\searrow$	$0$	$\nearrow$	$+\infty$

となる．ここで漸近線の方程式は
$y=\sqrt[3]{(x-1)(x-2)^2}\approx x\sqrt[3]{1-5x^{-1}}$ $\approx x\left(1-\dfrac{5}{3}x^{-1}\right)=x-\dfrac{5}{3}$
から $y=x-\dfrac{5}{3}$ であることに注意すると，グラフは次図