2022.09.01記
[3] 方程式 ノ表ハス曲線ヲ畫キ且其ノ長サヲ索メヨ.
ノ表ハス曲線ヲ畫キ且其ノ長サヲ索メヨ.
2022.09.06記
これは放物線の一部
[解答]
 は
は
 (
( )
)
と変形でき,これを原点のまわりに45度回転した図形は
 ,
,
とおくことにより
 ,
,
を用いて
 (
( )
)
つまり
 (
( )
)
となるので,これは放物線である. 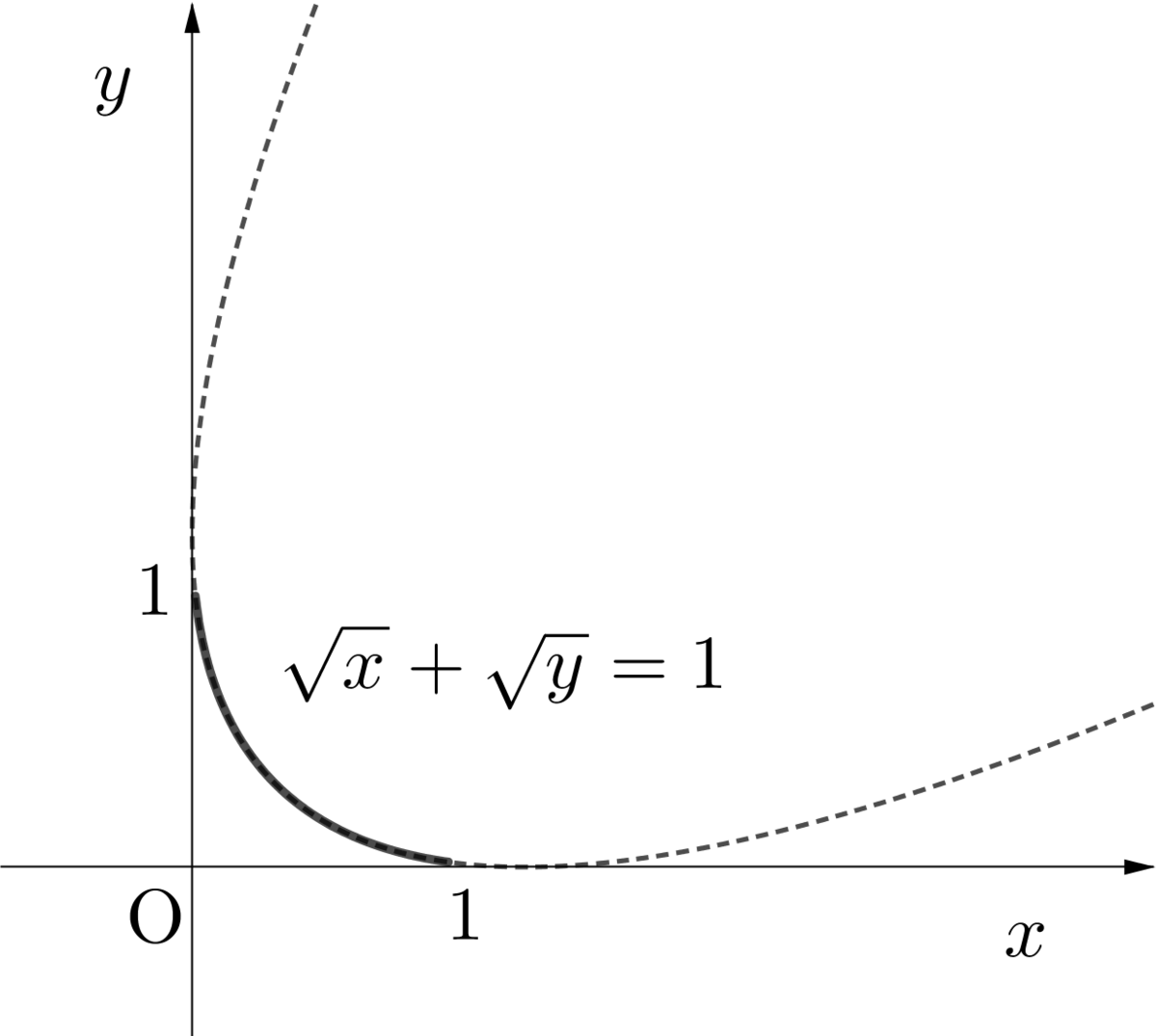
と変形でき,これを原点のまわりに45度回転した図形は
とおくことにより
を用いて
つまり
となるので,これは放物線である.

この曲線の長さは,
である.
と置換すると
であるから
なる
を用いて
となる.ここで から
となるので
(
)とパラメータ表示できるので,
を利用して弧長を求めても良い.