2023.08.29記
(i) ,
(ii) の任意の点
(
)に対し,
,
,
(iii) 人が三角形 の周を一周し,tex:\mbox{P}],
,
の順序に頂点を通るとき,三角形の内部は常に人の左側にある.
いま 上に相異なる二点
,
をとり,
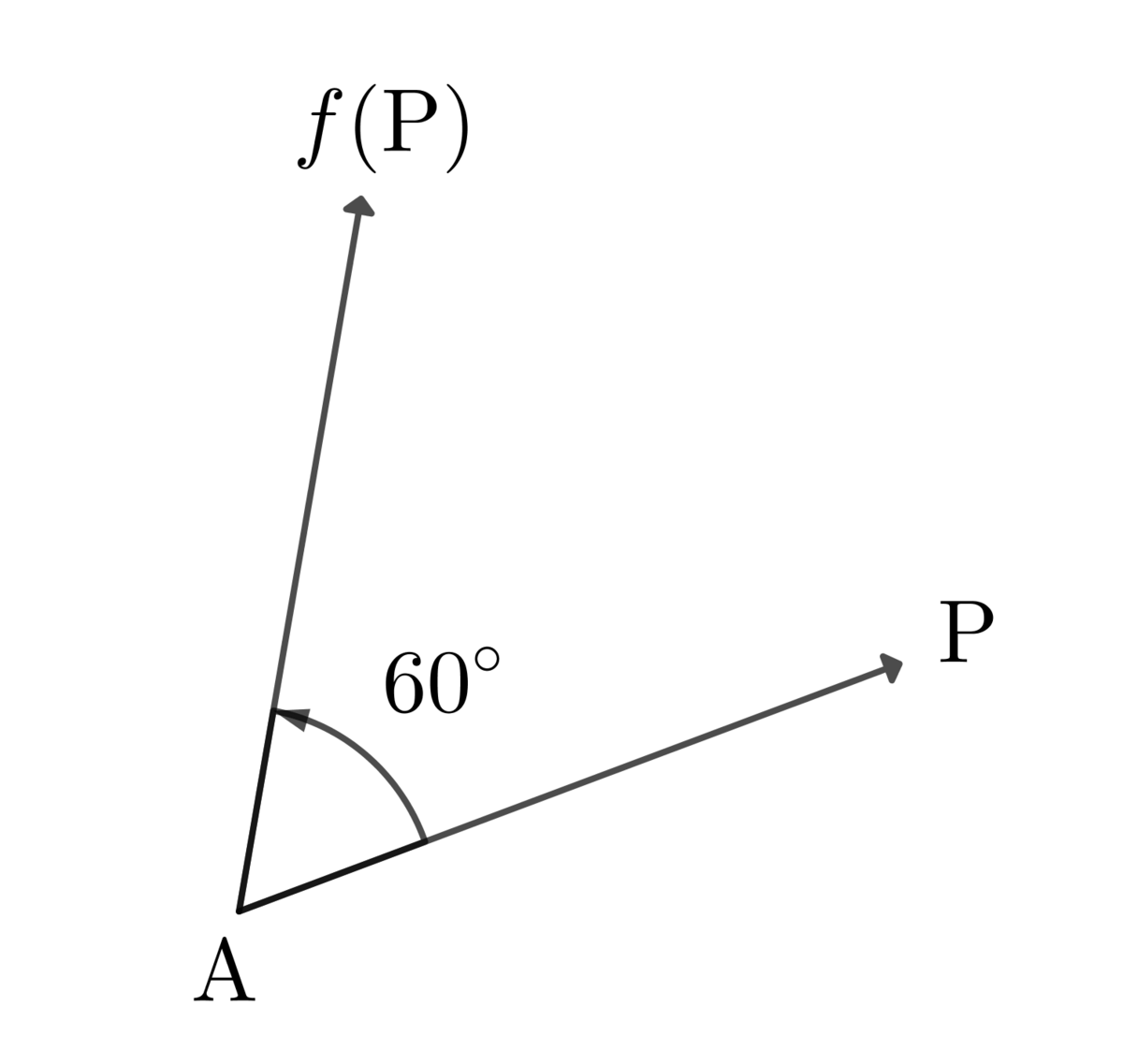
を中心とする正の向きの
回転を
,
を中心とする正の向きの
回転を
とする.これに対し,
と
の合成写像
が,
によって定義される.
(1) このとき,点 と
は,
,
に対して,どのような位置にあるかを求め,図示せよ.
(2) はある点
を中心とする正の向きの回転であることを示し,点
および回転角を求めよ.
2021.01.20記
回転の中心がどこであっても,ベクトルの向きは回転角だけで決まるので,
60度回転を2回続けて行うと,120度回転になる.
(1)
(2) の重心を
,
の重心を
とし,ベクトルを60度回転する行列を
とする.
は
を
に,
を
にうつすので,
を中心とする正の向き120度回転と予想できる.
平面上の任意の点 に対して,
が成立する.同様に,平面上の任意の点 に対して,
が成立する.よって として,
平面上の任意の点 に対して,
が成立する.
よって,平面上の任意の点 に対して,
は
を
中心に正の向きに120度回転した点となるので,
は
中心に正の向きに120度回転する変換である.
複素数でやると簡単である.
複素平面で考える.
の重心を
とし,
,
とすると,
は
中心に
を正の向きに120度回転した点だから
が成立し,よって
が成立する.
このとき, は
となるので は
中心に正の向きに120度回転する変換である.