1974年(昭和49年)東京大学-数学(理科) - [別館]球面倶楽部零八式markIISR

2023.08.09記

[1] 自然数 $n$ ， $p$ に対し， $n^p$ を十進法で書いたときの $1$ の位の数を $f_p(n)$ で表わす．ただし，自然数とは， $1$ ， $2$ ， $3$ ， $\cdots\cdots$ のことである．

(1) $n$ が自然数の全体を動くとき， $f_2(n)$ の取る値を全部求めよ．

(2) あらゆる自然数 $n$ に対して， $f_5(n)=f_1(n)$ が成りたつことを証明せよ．

(3) $n$ が自然数の全体を動くとき， $f_{100}(n)$ の取る値を全部求めよ．

[2] 長さ $l$ の線分が，その両端を放物線 $y=x^2$ の上にのせて動く．この線分の中点 $\mbox{M}$ が $x$ 軸にもっとも近い場合の $\mbox{M}$ の座標を求めよ．ただし $l\geqq 1$ とする．

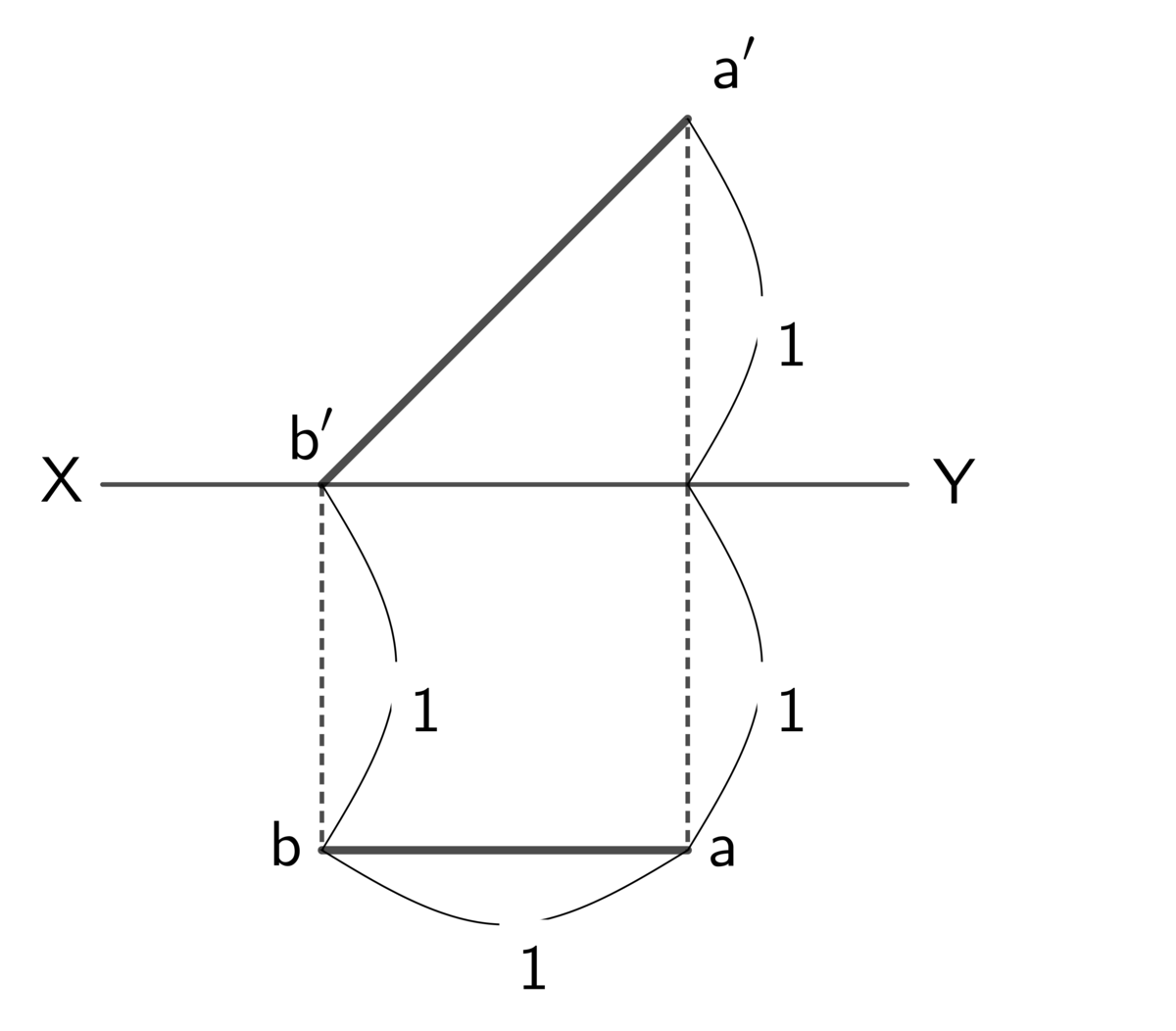
[3] 下の図は線分 $\mbox{AB}$ の投影図で，その各部の寸法は図に記入してある通りである．
この線分の上端 $\mbox{A}$ を通り， $\mbox{AB}$ となす角が $60^{\circ}$ ，平画面に対する傾きが $30^{\circ}$ であるような直線の，平画面上の跡を $\mbox{C}$ とする．点 $\mbox{B}$ の平面図 $\textrm{b}$ を原点とし， $\textrm{ab}$ を $x$ 軸， $\textrm{bb}'$ を $y$ 軸として，点 $\mbox{C}$ の座標を求めよ．

[4] 二つの関数 $f(x)$ ， $g(x)$ が次の性質 (1)，(2)，(3)，(4) を持つものとする．

(1) $f(x)$ ， $g(x)$ は $x=0$ において微分可能．

(2) $f(0)=g(0)=0$ ．

(3) 原点において， $y=f(x)$ および $y=g(x)$ のグラフに引いた接線はたがいに直交する．

(4) 実数 $a$ ， $b$ ， $c$ を適当に取ると，
$f'(0)=\displaystyle\lim_{x \to 0}\dfrac{ax+bf(x)}{cx+f(x)}$ ，
$g'(0)=\displaystyle\lim_{x \to 0}\dfrac{ax+bg(x)}{cx+g(x)}$ が成りたつ．

このとき， $a$ の値を求めよ．

[5] 原点 $\mbox{O}$ に中心をもつ半径 $2$ の固定された円板を $\mbox{A}$ とする．半径 $1$ の円板 $\mbox{B}$ を，その中心 $\mbox{C}$ が点 $(3,0)$ に重なるように置くとき，点 $(4,0)$ に重なる $\mbox{B}$ の周上の点を $\mbox{M}$ とする． $\mbox{B}$ を， $\mbox{A}$ の周囲に沿って滑らないようにころがして， $\mbox{OC}$ が $x$ 軸の正の方向となす角が $\theta$ になったときの， $\mbox{M}$ の位置の座標を $(\mbox{X},\mbox{Y})$ とする．

$\theta$ が $0$ から $\dfrac{\pi}{2}$ まで動くとして，次の問に答えよ．

(1) $\mbox{X}$ と $\mbox{Y}$ とを $\theta$ の関数として表わせ．

(2) $\mbox{Y}$ の最大値を求めよ．

(3) $\mbox{M}$ の描く曲線の弧の長さを求めよ．

[6] あるスポーツにおいて， $\mbox{A}$ ， $\mbox{B}$ 二チームが試合をして，さきに三回勝った方を優勝とする．一回の試合で $\mbox{A}$ が勝つ確率を $p$ ， $\mbox{B}$ が勝つ確率を $q$ （ $p+q=1$ ， $p\gt 0$ ， $q\gt 0$ ）とする．このとき， $\mbox{A}$ が優勝する確率を $P$ ， $\mbox{B}$ が優勝する確率を $Q$ とし，また，優勝チームがきまるまでの試合数を $N$ として，次の問に答えよ．