1992年(平成4年)東京大学前期-数学(理科)[4] - [別館]球面倶楽部零八式markIISR

2024.01.07記

[4] $xyz$ 空間において， $x$ 軸の平行な柱面
$A= \{ (x,y,z)\,|\, y^2+z^2=1$ ， $x$ ， $y$ ， $z$ は実数 $\}$
から， $y$ 軸と平行な柱面
$B = \{ (x,y,z)\,|\, x^2-\sqrt{3}xz+z^2=\dfrac{1}{4}$ ， $x$ ， $y$ ， $z$ は実数 $\}$
により囲まれる部分を切り抜いた残りの図形を $C$ とする．図形 $C$ の展開図をえがけ．ただし点 $(0,1,0)$ を通り $x$ 軸と平行な直線に沿って $C$ を切り開くものとする．

2020.09.26記
$A$ と $B$ の交わりは，定数項を消去して
$4x^2-4\sqrt{3}xz+3z^2-y^2=0$
から， $y=\pm(2x-\sqrt{3}z)$ となり，2平面上にあることがわかります．
よって，円柱面 $y^2+z^2=1$ を2平面で切った切り口について考えれば良いことになりますが、
円柱を(軸に垂直でない)平面で切った切り口にサインカーブが登場することは現在では常識です．

[解答]

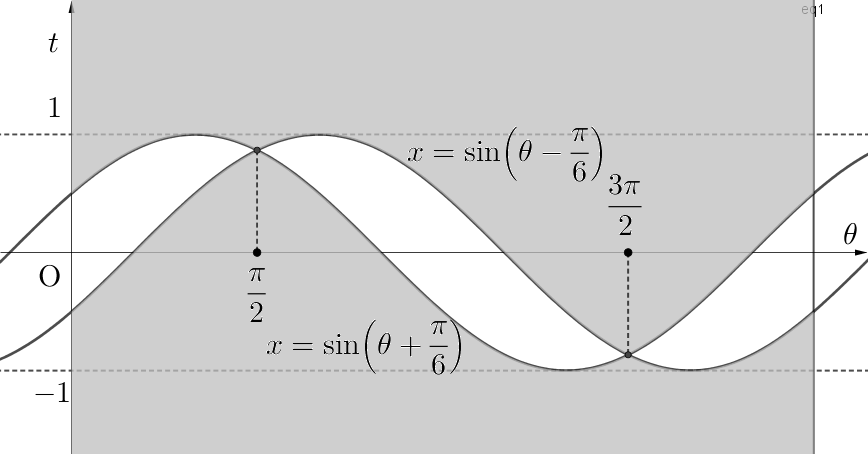
円柱面 $A$ の展開図の座標を $(\theta,t)$ とおくと，その3次元座標は $(t,\cos\theta,\sin\theta)$ となる．これが $B$ の外側（境界を含む）にある条件は
$t^2-\sqrt{3}t\sin\theta+\sin^2\theta\geqq\dfrac{1}{4}$

頑張って計算すると
$\Bigl\{t-\sin\Bigl(\theta+\dfrac{\pi}{6}\Bigr)\Bigr\}\Bigl\{t-\sin\Bigl(\theta-\dfrac{\pi}{6}\Bigr)\Bigr\}\geqq 0$
となるので，これを図示すると次のようになる．