2024.01.15記
(1) から
まで異なる番号のついた
個のボールを,
,
,
と区別された3つの箱に入れる場合,その入れ方は全部で何通りあるか.
(2) 互いに区別のつかない 個のボールを,
,
,
と区別された3つの箱に入れる場合,その入れ方は全部で何通りあるか.
(3) から
まで異なる番号のついた
個のボールを,区別のつかない
つの箱に入れる場合,その入れ方は全部で何通りあるか.
(4) が
の倍数
であるとき,
個の互に区別のつかないボールを,区別のつかない
つの箱に入れる場合,その入れ方は全部で何通りあるか.
[2] 辺の長さが
,
,
であるような鋭角三角形
の3辺
,
,
の中点をそれぞれ
,
,
とする.線分
,
,
に沿って三角形を折り曲げ,四面体をつくる.その際,線分
と
,
と
,
と
はそれぞれ同一視されて,長さが
,
,
の辺になるものとする.
(1) 線分 ,
の中点をそれぞれ
,
とする.四面体を組み立てたとき,空間内の線分
の長さを求めよ.
(2) この四面体の体積を ,
,
を用いて表せ.

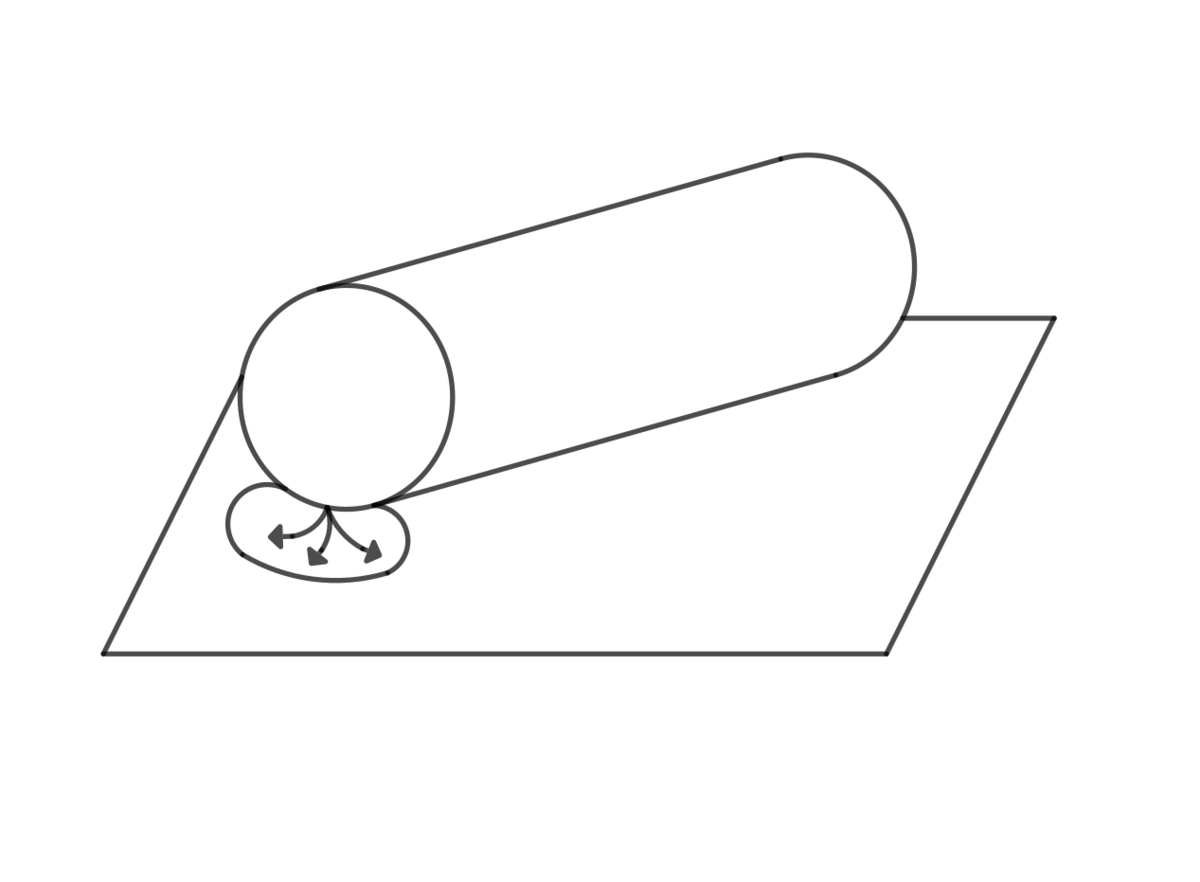
[3] 直円柱形の石油タンクが,図のように側面の一母線で水平な地面と接する形に横倒しになり,地面と接する一点に穴があいて石油が流出しはじめた.倒壊前の石
油タンクは一杯で,1時間後の現在までに半分の石油が流出した.単位時間当りの流出量は穴から測った油面の高さの平方根に比例するという.
微分方程式をたてて,このあと何時間何分で全部の石油が流出するか予測せよ.ただし,分未満は切り捨てよ.
https://spherical-harmonics.hateblo.jp/entry/Todai/1996/Kouki_1
https://spherical-harmonics.hateblo.jp/entry/Todai/1996/Kouki_2
https://spherical-harmonics.hateblo.jp/entry/Todai/1996/Kouki_3